[전공_시스템프로그래밍] 정수(Integer)의 연산
컴퓨터에서의 정수의 연산은 역시나 인간의 연산과는 다르게
인간이 처음 컴퓨터를 만들 때 정해놓은 방식과 그 한계에 의해서 왜곡되어서 표현된다.
1. 덧셈
정수의 덧셈은 이진수를 더하는 것과 같다.
실제로 컴퓨터는 ( u+v mod 2^32)로 계산이 된다.
여기서 주의해야할 점은 덧셈을 했을때 해당 워드 범위를 벗어나면 어떻게 되는지에 대해 알아야한다.

먼저 비부호형(unsigned)의 경우 워드범위를 벗어난 비트(캐리)는 버려진다.
예를 들면,

| 1111 + 1111 = 11110 = 1110 (2진수) |
위 예시와 그림처럼 캐리가 사라짐으로써 원래값보다 작아지는 것을 볼수있다.

다음으로 부호형 정수의 덧셈 역시 비부호형 정수와 비슷한형태로 이루어지는데,
맨앞의 캐리를 버린다는 개념은 동일하지만, 두가지 경우로 나누어진다.
양의 오버플로우, 양의 오버플로우
이 경우 맨 앞의 부호비트가 사라지기 때문에 값이 일반적인 계산값보다
급상승하거나 급하락하는 모양새를 보인다.
2의 보수 덧셈에서 오버플로우여부 판별조건을 간단히 살펴보면 아래와 같다.
| u, v < 0 | s >= 0 | 음의 오버플로우 |
| u, v > 0 | s <0 | 양의 오버플로우 |
2. 곱셈
곱셈도 어찌보면 덧셈이라 할 수 있는게,
곱셈은 그 비트수 만큼 덧셈을 한 것이기 때문이다.
So, 범위를 벗어난 캐리는 버려지게 된다.
예를 들면
int a, b, c;
c = a * b;
이런 경우 성립하게 되고,
다른 경우로
c = a * 5;
위와 같이 상수를 곱하는 경우는 Left Shift를 이용한 연산이 이루어 진다.
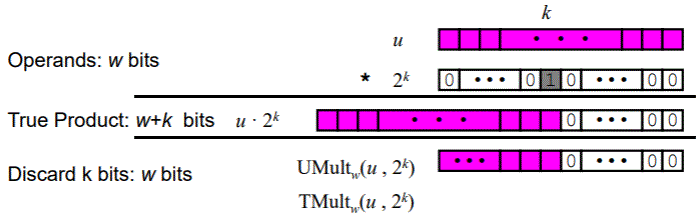
2^3 만큼 곱하는 연산은 << 3 이런식이다.
물론 캐리는 버린다.
3. 나눗셈
나눗셈의 경우 곱셈과 정반대 개념이므로
Right Shift를 적용하면 결과값을 얻을 수있다.

위 그림과 같이 비부호형의 나눗셈의 경우 오른쪽 쉬프트를 한 뒤 소수부를 버리면 된다.(논리 쉬프트 연산)

위 그림과 같이 부호형 정수의 나눗셈은 오른쪽 쉬프트를 한 뒤에 소수부를 "내림"한다. (산술 쉬프트 연산)
[출처]
위 게시물은 충남대학교 권진세 교수님의 강의자료와
네이버 블로그 {Edge Code}https://blog.naver.com/iws1605 의 설명을 참고하여 작성하였습니다.